
最后更新时间: 2018/09/05 11:34
数据结构是什么?
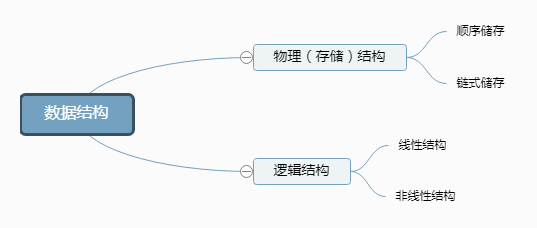
逻辑结构
数据之间的逻辑组织关系。 集合、线性、树形、图形
线性结构
逻辑上,一个接一个、有序的数据结构
比如:队列、栈、数组
特点:逻辑简单、存取方式简单
数组
是一种线性结构。按照一定的序,将同等类型的数据组织在一个集合内(collection。不同于set)
下标:数组内元素的编号。通常从0开始。
[学习链接](https://www.cnblogs.com/jiqing9006/p/7615467.html)
队列
是一种线性结构。按照FIFO(First-In-First-Out)方式来处理数据元素。
FIFO:先进先出。队列有头端(head)和尾端(tail),要进入队列的元素会被加入到尾端,而要出队列的元素则从头端离开。所以,尾端的元素在队列中的时间是最短的,头端的元素是待在队列红时间最长的。
栈
是一种线性结构。按照LIFO(Last-In-First-Out)方式来处理数据元素。
LIFO;后进先出。栈有两端,一个是栈底(bottom),一个是栈顶(top)。入栈和出栈的元素都是从栈顶来操作。所以,栈顶的元素在队列中的时间是最短的,栈底的元素是待在队列中时间最长的。
比如:一个瓶子,一颗接着一颗的往里放糖,要取下面的糖,必须先取出上面的糖。
jdk 核心线程池(execute)
资源 性能
并非级别 节点 现成
任务类型 计算密集 I/O密集 任务间依赖
用池 进行管理
非线性结构
逻辑上、1对多、多对1、多对多的数据结构
比如:树、图、超文本(适合跳转)
特点:灵活、存取方式较复杂
树
一个由有限个节点组成的有层次关系的数据结构
节点:每个元素称为节点
根:所有节点的共同祖先
子树:除根节点外,其他的元素的集合如果也可以组成一颗树
度:一个节点含有的子树的个数
树的度:所有节点中最大的度
叶子节点:度=0的节点
分支(非叶)节点:度!=0的节点
树高或者树深:树的最大层次
二叉树
是一颗树,每个节点最多有两个孩子。
二叉树可以是空树,左、有子树可为空,也可以不为空。
二叉树的应用意义:
层次化组织:继承了树的优点,解决数据量大时,链表的线性访问的效率低的问题。
分类判定:分叉的性质可以处理分类的问题,分类就是一种判定问题,这在人工智能判定和游戏设计中的判定中非常有用。
排序优化:采用完全二叉树或类完全二叉树的堆进行排序优化,效率很高。
平衡树:通过降低树的层次保持平衡,如:AVL树,RB树,对非随机二叉树的优化使得天然地能高效处理增、删、改、查。
数据压缩:gzip、zip、png图像的压缩算法,deflate算法中利用huffman树进行二次压缩。
二叉树的遍历:
先序遍历递归算法:
访问根节点;访问左子树;访问右子树;
中序遍历递归算法:
访问左子树;访问根节点;访问右子树;
后序遍历递归算法:
访问左子树;访问右子树;访问根节点;
满二叉树:节点数为满(2^N-1)的二叉树,N表示层次
完全二叉树:
除了最后一层外,其他层的节点都满
Huffman Tree 哈夫曼树(最优二叉树)
gzip、png压缩中应用
Binary Heap 二叉堆,
优先队列、堆排序
二叉搜索树
递归定义:
T是一颗空树,
如果该树的左子树不为空,则有左子树所有的key,都小于或者等于根的key
如果该树的右子树不为空,则有右子树所有的key,都大于根的key
左子树和右子树同时也是一颗二叉搜索树
AVL Tree 平衡二叉搜索树
一种自平衡二叉查找树,一种面向内存的数组结构。
如何判断是否为AVL树:
T是空树
T若不是空树,则右子树、和左子树都是AVL树,且|左子树高度-右子树高度|<=1

平衡因子:一个节点的左子树的高度减右子树的高度。如果取值在(-1,0,1)中,则树是平衡的。
AVL树的特点:
1.自平衡,即每次插入和删除元素时,如果树不平衡,则通过旋转来使树重新平衡。平衡的目的是通过降低树的高度,减少平均查找长度。
2.N个元素的AVL树高O(logN)
3.N个元素的AVL树平均查找、插入和删除效率都是O(logN)
4.二叉树的查找算法适用于AVL树
例子:

Red Black Tree 红黑树(应用广泛)
读多写少的大量数据场景
写多的场景nginx、linux:vma查找
Binary Decision Tree 二叉判定树
条件判定、分类、人工智能判定、游戏中的情景判定
一对多的关系
多叉树
B、B+、B*tree 文件系统、数据索引(一堆数据)
B+树
B是Balanced,平衡的,一种面向磁盘的数据结构
所有的叶子结点在同一层
内部节点本身存储了数据
关键字按升序排列
整棵树只有1个节点时,根节点就是叶子节点,否则,根节点的孩子个数:2<= b<= m
内部节点的孩子个数:[m/2]<= b <= m
内部节点的关键字个数:[m/2]- 1<= b<= m-1
用来解决什么问题?
磁盘I/O特性;
1.随机慢于顺序;
2.寻道时间是最主要性能瓶颈
3.依次读取一个或多个连续的页面来摊还寻道时间;
4.存取时间在特殊情况下比内存慢万倍。
B+树
结构特性,结合mysql中innerDB引进组织方式来分析B+树的实际数据库设计中的表现,最后介绍facebook处理FTS(全表扫描)的效率上的一些优化。
存储(物理)结构
数据在计算机内:二进制、十六进制。
关系在计算机内:顺序(相对位置) 非顺序(指针)
顺序存储结构
在物理上,利用一片连续、相邻的空间存放数据。
特点:知道索引后,适合随机查找、适合连续RW的场景、充分利用连续的内存、磁盘空间来访问数据、避免多次磁盘寻道以节约时间
链式存储结构
在物理上,利用不连续,随机、零碎的空间来存放数据。
特点:适合频繁的更新、删除,随机RW场景,根据实际需要动态地分配存储空间,空间利用率高。

图
线性结构研究的是一对一的关系
树形结构研究的是一对多的关系
图研究的是数据元素之间多对多的关系
有向图 和 无向图
最小生成树(满足最小代价)、最短路径的意义和算法思想
图的存储方式和图的遍历
邻接表法:
用一个数组存储所有的顶点,对每个顶点,用一个链表存储该点的临接点。
邻接矩阵法:
使用一个二维数组A[][],对于一个边(u,v),置A[u][v]=1,否则就置A[u][v]=0
对于带权图,可以置A[u][v]=weight,weight表示权重。
优点:直观,适合稠密图
缺点:如果图的变数很少,或者说图是稀疏的,浪费很多空间
将图看作为二元组,V(vertex)是定点集,E(edge)是边集,每条边就是一个顶点对(v,w)
生成树是包含了图的所有顶点的连通子图
TSP(旅行商)的问题
并利用只能搜索算法中的遗传算法求TSP问题的近似解。结合图中最优路径、NP难题以及智能算法的扩展。
数据结构有什么用?
数据的存储方式影响着有关处理的效率
顺序>连续>RW、 非顺序>随机RW
数据的结构一旦确定,往往算法也跟着确定
栈>递归、 环形队列>消息缓冲
数据结构启发着思维方式
Zookeeper.2pc.DQ、 DL、 RW-L
常用的数据结构
链表
双向循环链表、单向循环链表
堆
海量数据,大文件分为小文件排序
图
散列
抽象数据类型
线性表(List) 表结构
特征: 一对一关系
ArrayList 基于数组实现
顺序存储方式线性结构
存储位置连续,
ArrayList
arraylist代码查看
链式存储方式线性结构
LinkedList 存储单元可以是连续的,也可以是不连续的
优点;插入删除效率高
缺点:查询效率低
linkedList代码查看
toArray()
线性表——栈——推荐使用顺序存储结构
允许插入和删除的一端成为栈顶(Top),另一端称为栈底(bottom),不含任何数据元素的栈称为空栈,栈又称为后进新出的线性表
AbstraList
exctend
Vector
exctend
Stack
中缀表达式——标准四则运算表达式
9+ (3-1) *3+10/2
后缀表达式——计算机采用
1 | 931-3*+10 2/+ |
中缀表达式转后缀表达式,利用栈解决
线性表——队列——推荐使用链式存储结构
只允许在一端进行插入删除,而在另一端进行删除操作的线性表。插入一端称为队尾,删除的一端称为队头
队列的顺序存储以及结构模式
缺点:出队复杂度高0(n)
容易假溢出
解决方案:
循环队列,把队列的这种头尾相接的顺序存储结构称为循环队列。
队列的链式存储以及结构模式
队列的链式存储结构,其实就是线性表的单链表,只不过它只能尾近头出而已。